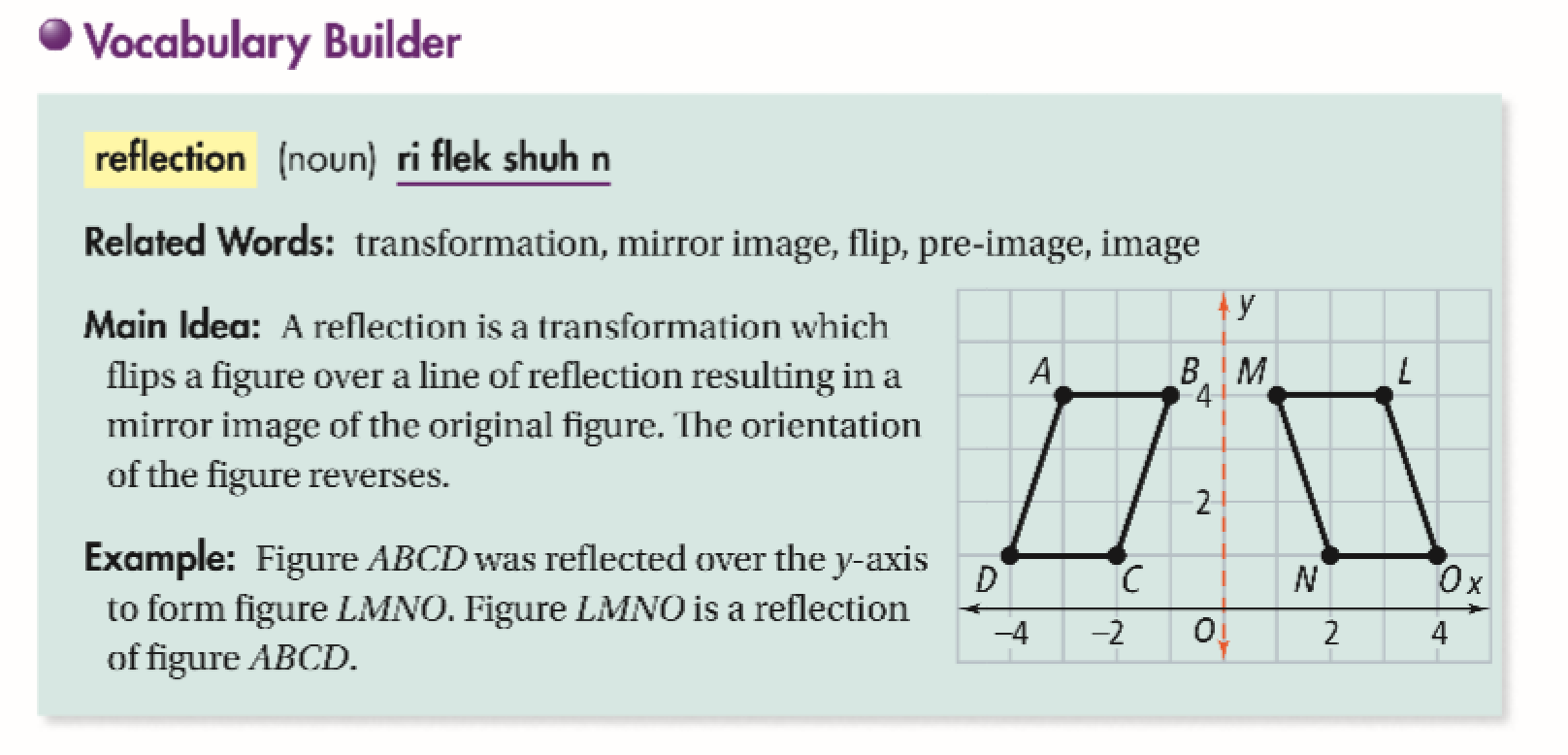
上 reflection over line y=x 198175-Reflection over line y x
Graph the line Ask students to start with point A and reflect it over the line My students told me to go left 2 squares to get to y = xx and then 2 more squares past that to create the new line While this is the method we learned for reflecting points over a line, we always had a horizontal or vertical line, not a diagonal lineWe can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the x axis, or the line y = 0 Here are the graphs of y = f ( x ) and y = f ( x )We're asked to use the reflection tool to define a reflection that will map line segments Emme line segments Emme on to the other line segments below so we want to map Emme to this segment over here and we want to use a reflection let's see let's see what they expect from us if we want to add a reflection so if I click on this it says reflection over the line from and then we have two

Reflection Over The Line Y X Geogebra
Reflection over line y x
Reflection over line y x-A reflection is a "flip" of an object over a line Let's look at two very common reflections a horizontal reflection and a vertical reflection Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change size
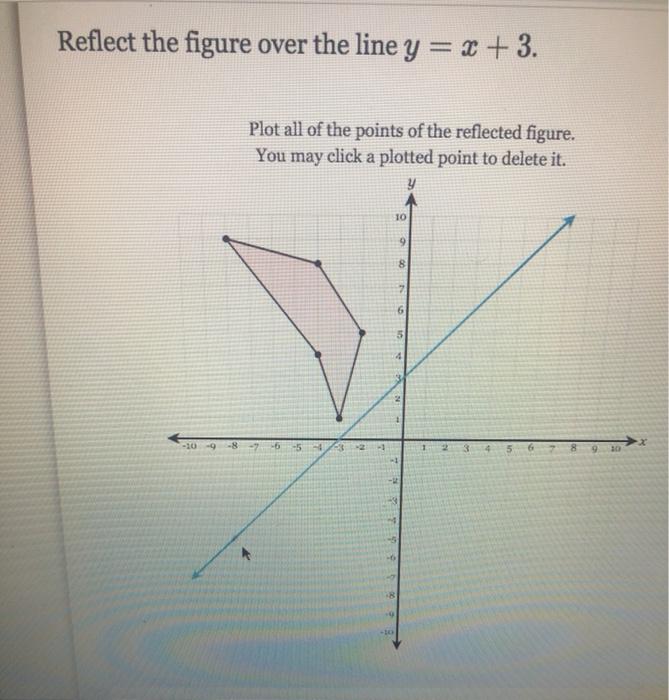



Solved Reflect The Figure Over The Line Y X 3 Plot All Chegg Com
If you reflect over the line y = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed) What happens when an ordered pair is reflected over any line?A reflection of a point over the line y = − x y = −x is shown The rule for a reflection in the origin is (x, y) → (− y, − x) Explanation It's astonishing how difficult it is to find a good explanation how to reflect a point over a line that does not use higher math methods So here is my explanation From the diagram we see the object point ( − 2, −5) is mapped to (x',y') by a reflection in the line X = 2 we note (1) the ycoordinate is unaffected (2) for reflections the distance from the line of reflection to the object is equal to the distance to the image point ∴ a = 2 2 = 4units so the image point is 4 units from the line of
This brief video explores reflecting an image over the y=x and the y=x lines, with the coordinate rules for bothReflect over the xaxis (x, y) > (x, y) Reflect around the origin (x,y) > (x, y) Reflect over the line y = x (x, y) > (y, x) Reflection an image flipped over a line A triangle reflected over the xaxis Translation an image slides left or right, up or down Translated 4 units left (x, y) > (x4, y) Translated 3 units down (x, y) > (xSubjects Arts and Humanities Languages
Reflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the point anywhere you wantPrecalculus 1 Answer Jim G image A' = (5 , 3 ) Explanation Any point (x , y ) when reflected in the line y = x has an image ( y , x ) example A (3 , 4 ) has image A' ( 4 , 3 ) Answer link Related questionsExplanation the line y=1 is a horizontal line passing through all points with a ycoordinate of 1 the point (3,10) reflected in this line the xcoordinate remains in the same position What does it mean to reflect over Y 0?
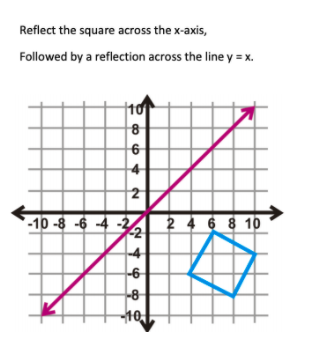



Solved Reflect The Square Across The X Axis Followed By A Chegg Com




Reflection Transformation Matrix
Answer (1 of 2) There are at least two ways of doing so Method 1 The line y = 3 is parallel to xaxis Let the required image is P′ By common sense, we know (Distance between the line y = 3 and point P) = (Distance between line y= 3 and point P′) Since line joining PP′ is perpendicular toFirst shift three units to the left, so the line of reflection becomes the y axis, then flip, and finally remember to shift three units back to the right to put the center line back where it belongs (This gives the f ( 6 − x) solution you already know) Replace x with 6 − xReflection in the line y = 0 ie, in the xaxis The line y = 0 means the xaxis




Reflection




How To Find The Equation Of The Graph Reflected About A Line Mathematics Stack Exchange
Apply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the To reflect over a vertical line, such as $x=a$, first translate so the line is shifted to the yaxis, then reflect over it, then translate back so the line is shiftedReflect over line y = x Reflect over the x axis alternatives Reflect over the yaxis Reflect over line y = x Reflect over line y = x answer explanation s Topics Report an issue Quizzes you may like 10 Qs The Mystery of King Tut 13k plays 15 Qs Egyptian Mummification




Picture Of Reflection In The Line Y X Reflection Math Common Myths Types Of Reflection



Translation Math
Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure What does it mean to reflect over Y 1?3 people liked this ShowMe Flag ShowMe Viewed after searching for reflection over the line y=x reflection over yaxis Reflection over y=x is over of equals percent over 100 reflect over x= 1 You must be logged into ShowMe



What Does It Mean To Reflect Over The Y X Line Quora



Reflection Of A Point In A Line Msrblog
A reflection of a point over the line y = − x is shown The rule for a reflection in the origin is ( x , y ) → ( − y , − x ) Subjects Near Me Series 52 Test Prep Research Writing Tutors IB Visual Arts SLThe handout, Reflection over Any Oblique Line, shows the derivations of the linear transformation rules for lines of reflection y = √(3)x – 4 and y = 4/5x 4 Line y = √(3)x – 4 θ = Tan1 (√(3)) = 60° and b = 4 The corresponding linear transformation rule is (p, q) → (r, s) = (05p 0866q 3464, 0866p 05q – 2Answer (1 of 3) This is a method used to find the reflection over the line y = x, aka finding the multiplicative inverse of elementary functions for a function y of x, switch your x and y variables solve for y That gives us the reflection For example, if we had y = 3x 6, switch x and y




S1 Work For Problem Ii About Reflection Respect To The Y X Line But Download Scientific Diagram
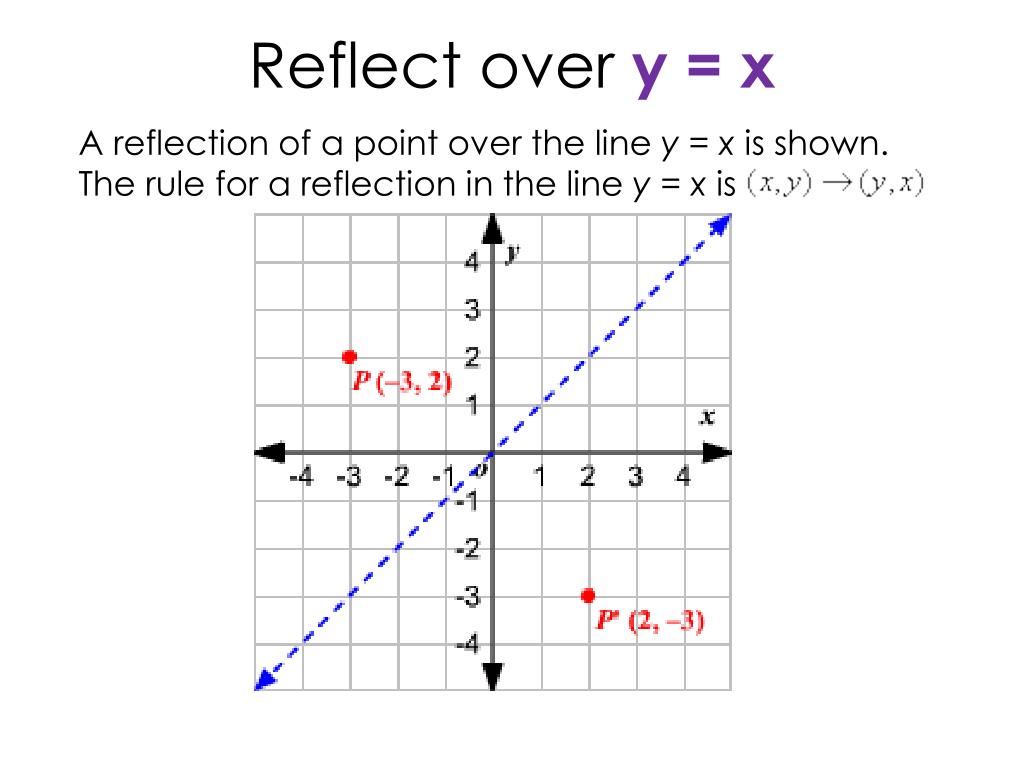



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id
And also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxisReflect over line y= x (y,x) The line of reflection a line that acts as a mirror so that corresponding points are equidistant from the line The line drawn between corresponding points in a reflection should always be _____ to the line of reflection perpendicular; What is #A'#, the image of #A(3,5)#, after a reflection in the line #y = x#?




Reflection Transformation Matrix




Reflection In Geometry Examples Solutions Videos Worksheets Games Activities
Answer (1 of 10) Here is another elegant way of looking at this, in addition to the answers below which are all correct Given a point (x, y) , we want a point (y, x) So, the question is \forall (x, f(x)) , what is the line of symmetry, \ni , (f(x), x) is constructed Notice the distance beReflection over x axis and y axis When P(x, y) is reflected in the mirror line to become p'(x', y'), the mirror line perpendicularly bisects pp' Thus, for every point of an object, the mirror line is perpendicularly bisects the line segment joining the point with its imageAnswer (1 of 4) You really need to draw this out to get a real feel for the answer and what is happening Think of y=2 as a horizontal mirror line Cutting through the yaxis at 2 The point (3,1) will reflect from below the xaxis over the mirror line and end up, above it, keeping the xcoor



1



Assignment 2 Transforming Parabolas
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x"a translation of (x, y) → (x 1, y 5) after a reflection in the line y = x" You may also see the notation written as This process must be done from right to left Composition of transformations you could reflect over y = _____ and then y = 25 17 19 Determine the missing line of reflection Draw it in and complete the compositeGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha



Solved Graph A Triangle Label It Lmn And Reflect It Over The Line Y X To Create Triangle L M N Describe The Transformation Using Words Draw Course Hero
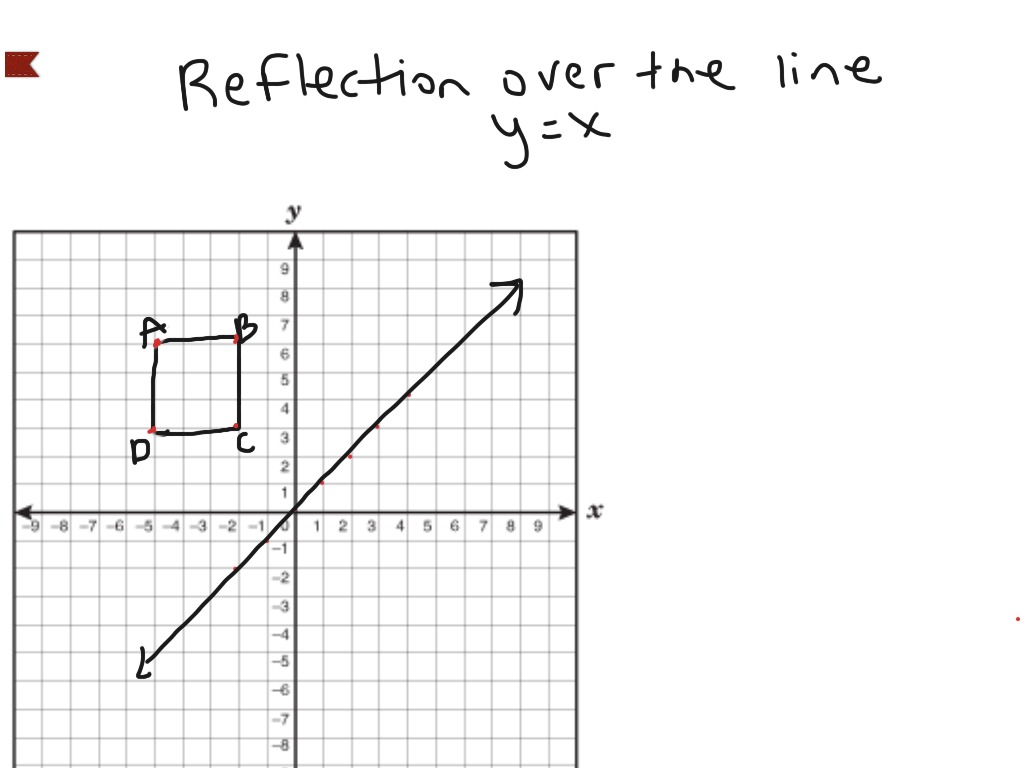



Reflection Over The Line Y X Math Showme
Answer (1 of 4) The line that represents y=x has a slope of 1/1 If i am considering a point, ill refer to it as A at (4,3) and reflect it over line y=x i will be at (4,3) which i will refer to as point B I can prove this relationship using simple geometry I will select a point on line y=x illPlay this game to review Geometry B(2, 4) Reflect over the line y = x Preview this quiz on Quizizz B(2, 4)Reflect over the line y = x Reflections over y = x and y = x DRAFT 8th grade 274 times Mathematics 54% average accuracy 10 months ago jnugeness 0 Save Edit Edit Reflections over y = x and y = x DRAFT 10 months ago byReflecting shapes diagonal line of reflection Our mission is to provide a free, worldclass education to anyone, anywhere Khan Academy is a 501(c)(3) nonprofit organization
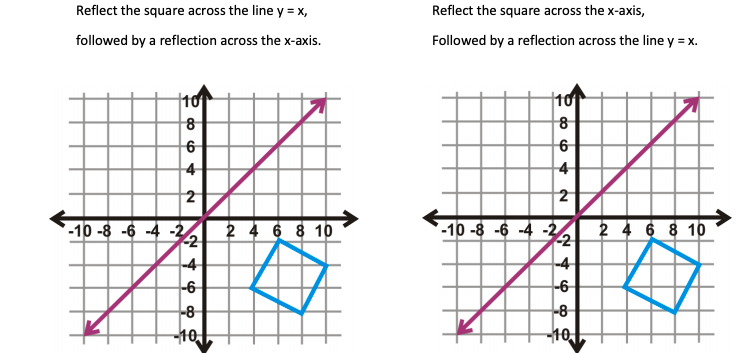



Solved Reflect The Square Across The Line Y X Followed By Chegg Com




Write The Coordinates Of The Vertices After A Reflection Across The Line Y X Brainly Com
Answer Stepbystep explanation Reflection of (8 , 1) over y = x is (1 , 8) Image of (x , y) over the line y = x is (y, x)This is a KS3 lesson on reflecting a shape in the line y = −x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = −x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendableReflect over the xaxis When you reflect a point across the xaxis, the xcoordinate remains the same, but the ycoordinate is transformed into its opposite (its sign is changed) If you forget the rules for reflections when graphing, simply fold your paper along the xaxis (the line of reflection) to see where the new figure will be located Or you can measure how far your points are away




Solved Reflect The Figure Over The Line Y X 3 Plot All Chegg Com



What Is The Image Of 2 5 Reflected Across X 2 Socratic
Point (x,y) reflects to point (x,y) Reflection over y axis (line of reflection y axis) Reflection over line y=x or y=Reflection over line y=x or y=xx For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflectionLine segments I end this segment i n over here and T oh this is T oh here are reflected over the line y is equal to negative X minus 2 so this is the line that they're reflected about this dashed purple line and it is indeed y equals negative X minus 2 this right over here is in slopeintercept form the slope should be negative 1 and we see that the slope of this purple line is indeed negative
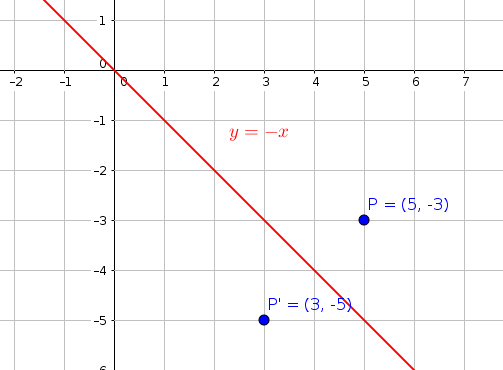



What Is The Reflection Image Of 5 3 In The Line Y X Socratic




How To Find A Reflection Image
Reflecting over any line And also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxisAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators



Geometric Reflections Q35 50 Intro To Geometry




Common Reflections Key Stage 3



1



2



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N




Reflection Over The Y X Line Youtube




How To Find A Reflection Image




Reflection Mathbitsnotebook A1 Ccss Math



Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Reflection In The Line Y X Geogebra



1




Reflection Over The Line Y X Geogebra




Transformations Of Graphs




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




What Is A Line Of Reflection Printable Summary Virtual Nerd




Reflection Mathbitsnotebook A1 Ccss Math
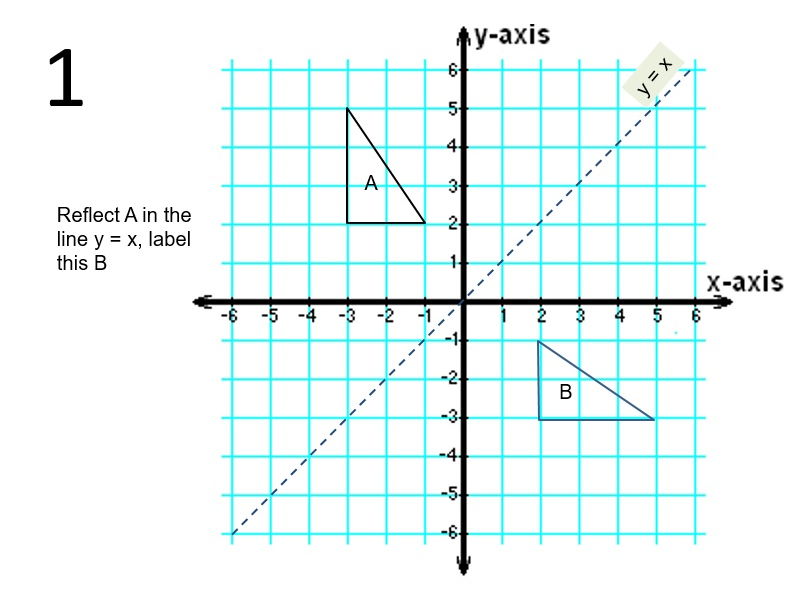



Diagonal Reflections In The Line Y X Teaching Resources




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Reflection Over The Line Y X Math Showme




Reflection Over Y 2 With Rule Educreations



Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative




Which Graph Shows A Reflection Across The Line Y X Brainly Com



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q




Transformation Reflection Over The Line Y X Youtube




Let T R2 R2 Be A Reflection In The Line Y X Find The Image Homeworklib
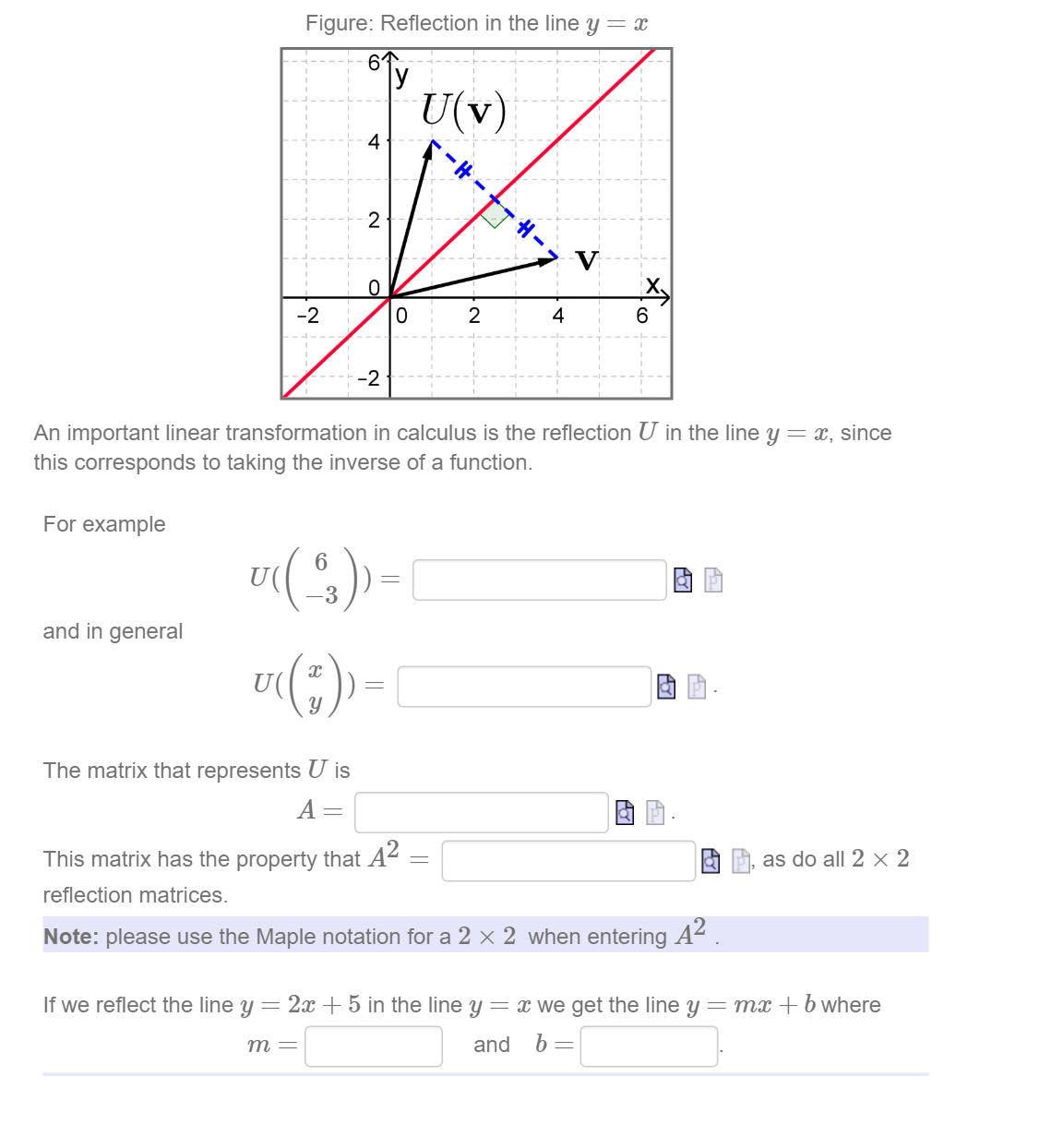



Solved An Important Linear Transformation In Calculus Is The Chegg Com




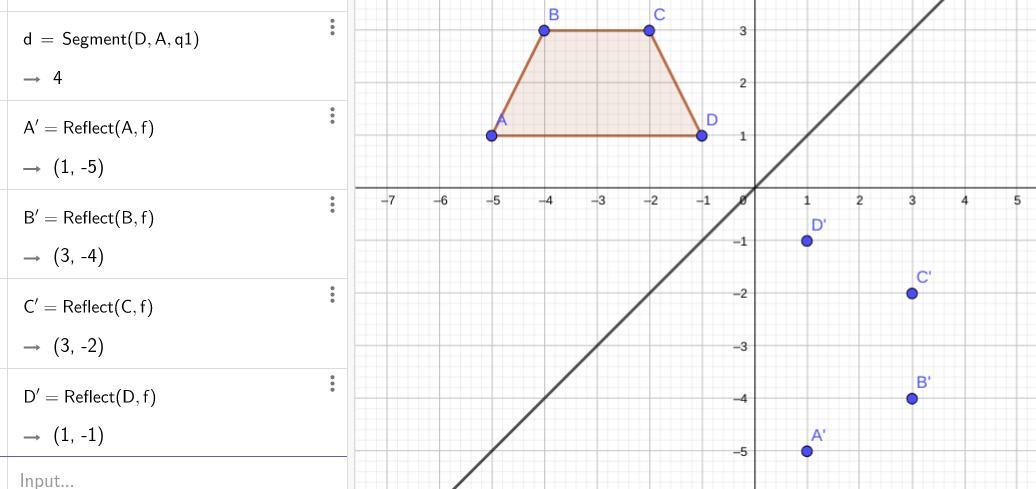
02 02 Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Brainly Com



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download




Reflections Of Functions



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Picture Of Reflection Across Y Axis Reflection Math Math Reflection




Geometry Transformations
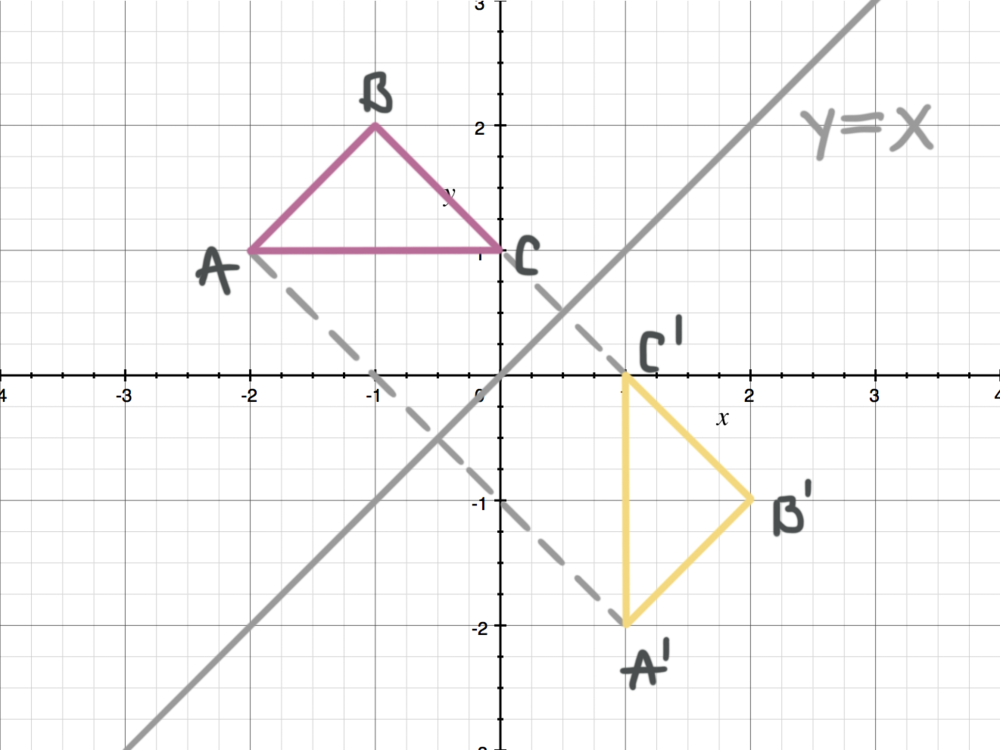



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
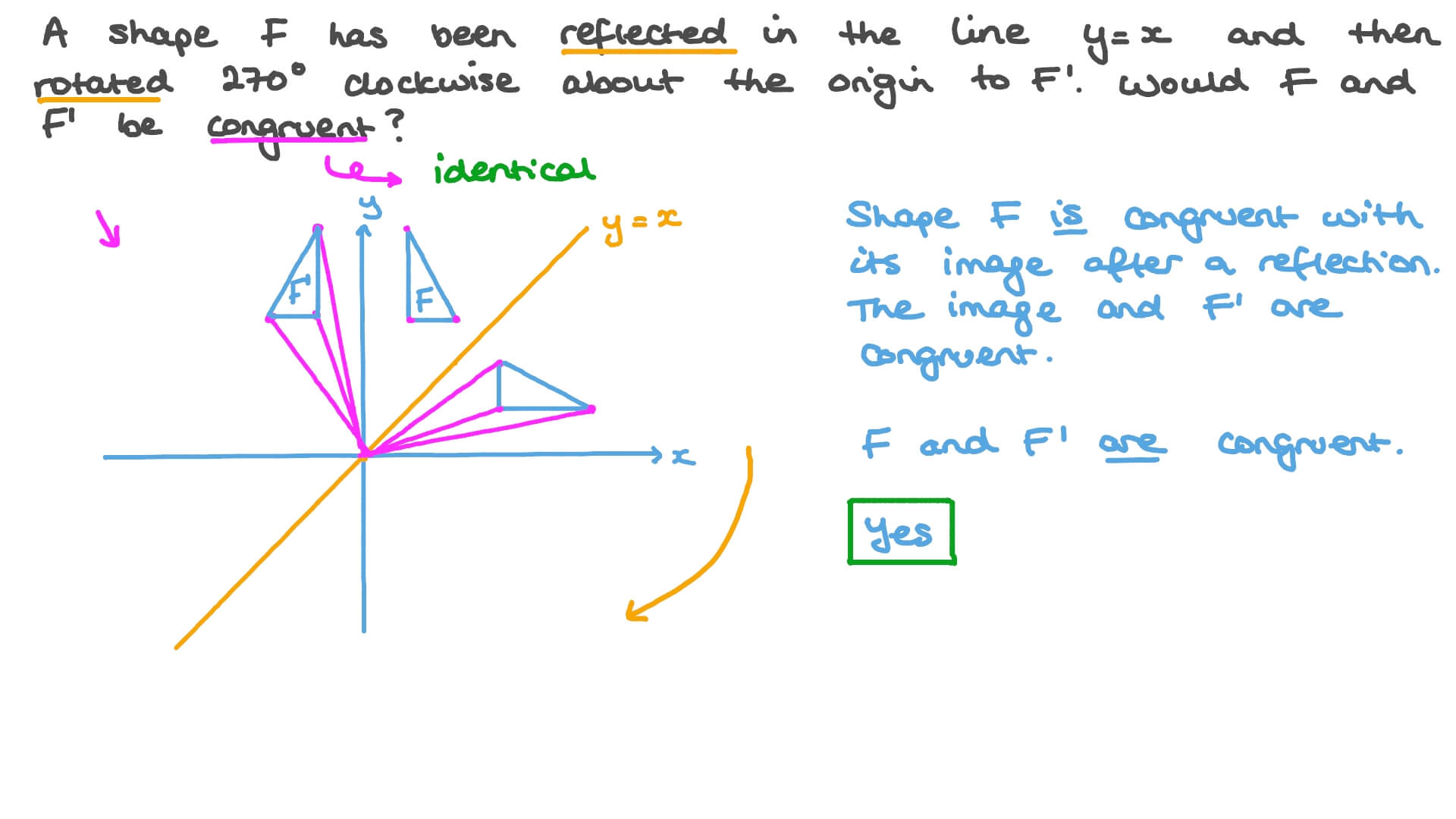



Question Video Understanding The Effects Of Reflection And Rotation On A Shape Nagwa
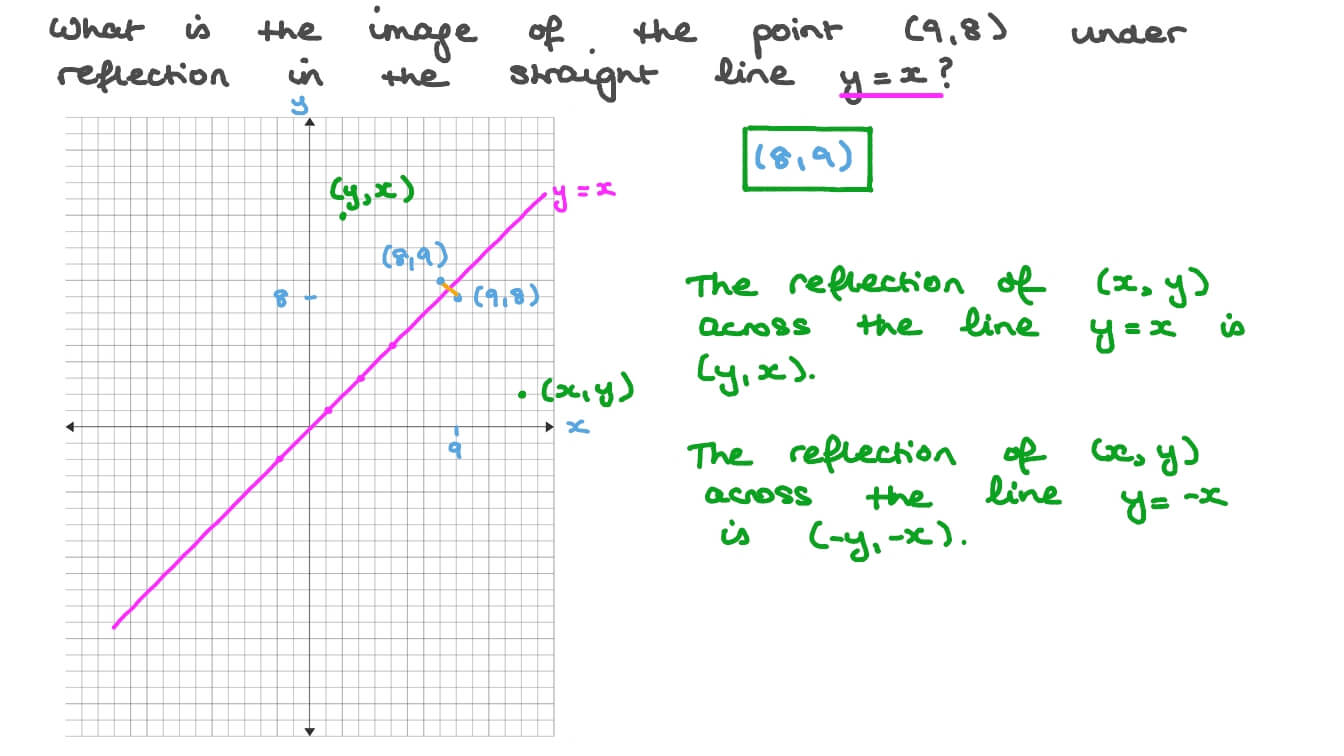



Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa




Ixl Reflections Find The Coordinates Grade 7 Maths Practice




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic



Solution What Is The Image Of A 3 1 After A Reflection First Across The Line Y 3 And Then Across The Line X 1
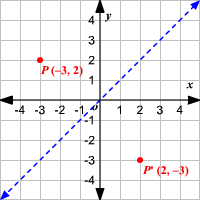



Reflections



Reflections Review Article Reflections Khan Academy




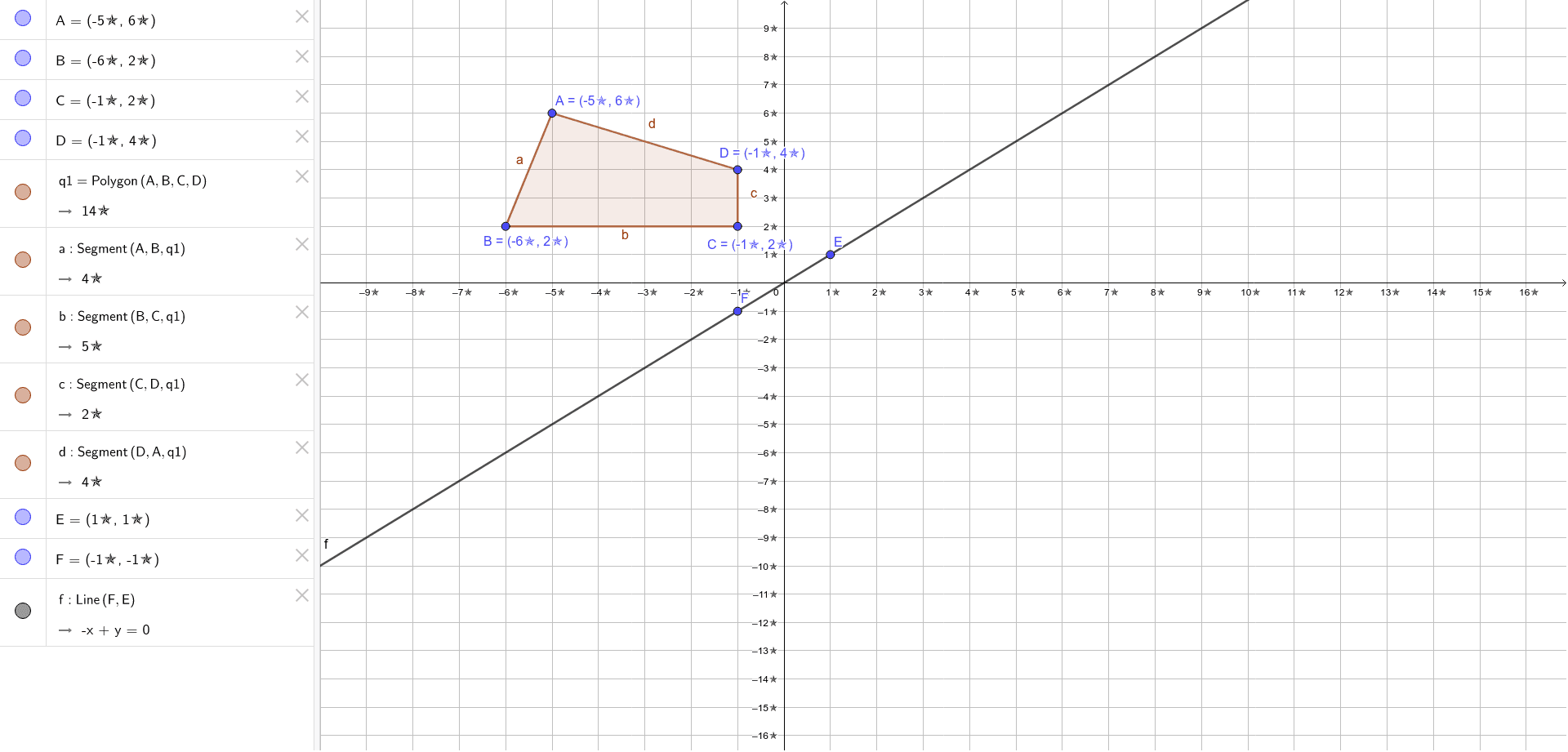
Kite Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection Brainly Com



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



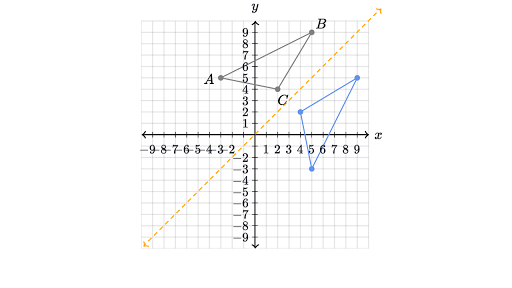
Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection And What Is The New Coo



Reflection Across The Line Y X Geogebra



2




Reflections Geometry Abroad




Reflection Objectives D Grade Reflect Shapes In Lines




Reflection Transformation Matrix




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Mathbitsnotebook A1 Ccss Math




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Geogebra Project Rotations And Reflections Math At Dis




How Are We Studying Transformations Differently By Eureka Math Eureka Math Medium




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
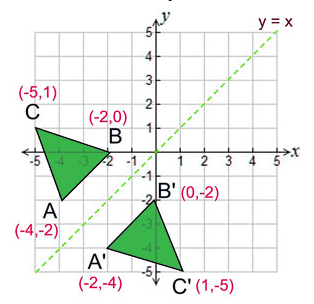



Reflection Definition Reflection In The Coordinate Plane



Math Alive Geometry 1




Learn About Reflection Over The Line Y X Caddell Prep Online




Reflection In The Line Y X Transformation Matrix Youtube
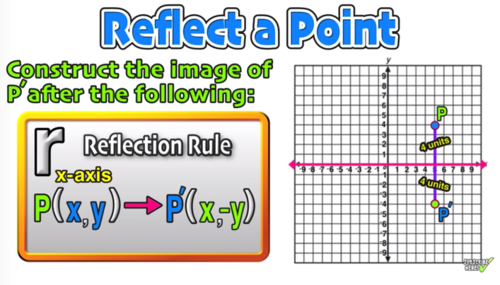



Reflection Over The X And Y Axis The Complete Guide Mashup Math




10 Math Problems Transformation Reflection



Math Alive Geometry 1



Illustrative Mathematics




Transformations Boundless Algebra




Reflection Over The Line Y X Youtube
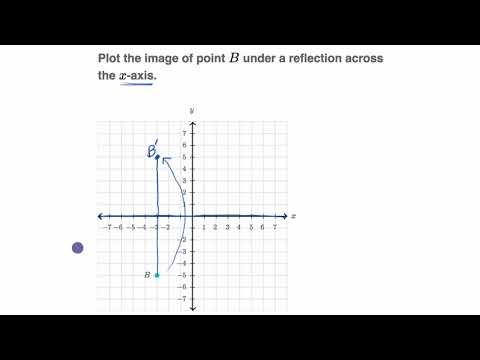



Reflecting Points Video Reflections Khan Academy




Reflections Ck 12 Foundation
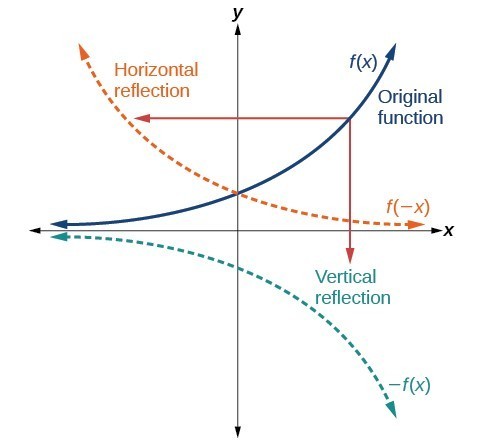



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
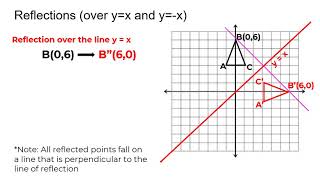



Reflection Over The Y X Line Youtube
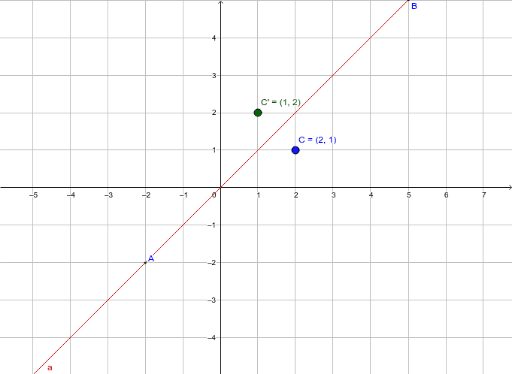



Reflection Across Y X Geogebra




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
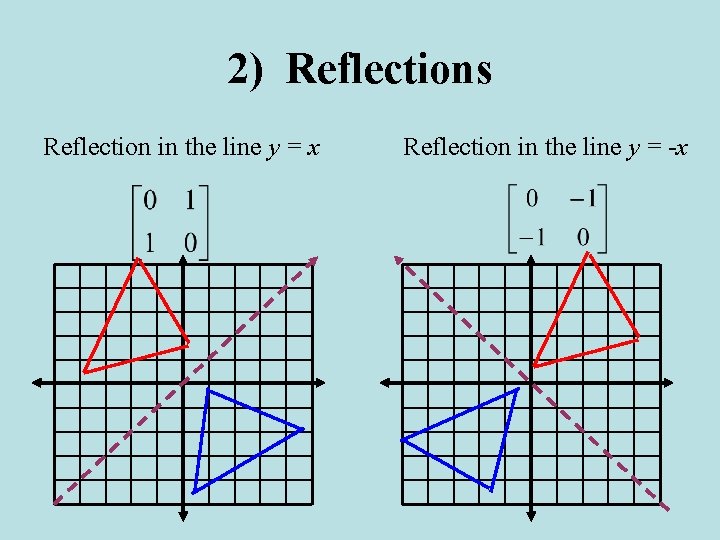



4 4 Transformations With Matrices 2 Reflections And




Reflections Across Y X Geogebra



Chapter 8 Page 460




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




10 Math Problems Transformation Reflection




Reflection Over A Line Expii




Reflections Ck 12 Foundation
コメント
コメントを投稿